You are here: Foswiki>Cosmo Web>WebPreferences>CosmoProjectsBrief>CosmoCurvature (06 Sep 2010, BoudRoukema)Edit Attach
<< Cosmo
 This mainly includes
This mainly includes 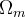 and
and 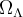 . The first (and possibly the only, so far) simultaneous constraint on both
. The first (and possibly the only, so far) simultaneous constraint on both 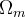 and
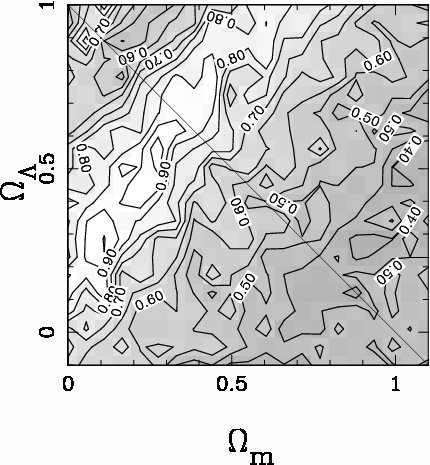
and 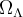 from within a single survey, using a standard ruler method, is AstroPh:0106135 - Roukema, Mamon, Bajtlik (2002). This topic is generally referred to today as BAO - the use of baryonic acoustic oscillations - although in fact can be more general, i.e. make less assumptions. The best-cited example of BAO usage is AstroPh:0501171 SDSS z < 0.47 Eisenstein et al., who estimated Omega_total = 1.010\pm0.009. Updating Roukema, Mamon & Bajtlik (2002) on newer QSO redshift surveys should result in preciser, and hopefully more accurate, estimates of these metric parameters.
from within a single survey, using a standard ruler method, is AstroPh:0106135 - Roukema, Mamon, Bajtlik (2002). This topic is generally referred to today as BAO - the use of baryonic acoustic oscillations - although in fact can be more general, i.e. make less assumptions. The best-cited example of BAO usage is AstroPh:0501171 SDSS z < 0.47 Eisenstein et al., who estimated Omega_total = 1.010\pm0.009. Updating Roukema, Mamon & Bajtlik (2002) on newer QSO redshift surveys should result in preciser, and hopefully more accurate, estimates of these metric parameters.
Cosmic Curvature (standard ruler)
Some of the most important parameters of the metric are those that directly affect the curvature of three-dimensional comoving spatial sections. This mainly includes
This mainly includes 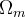 and
and 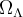 . The first (and possibly the only, so far) simultaneous constraint on both
. The first (and possibly the only, so far) simultaneous constraint on both 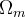 and
and 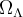 from within a single survey, using a standard ruler method, is AstroPh:0106135 - Roukema, Mamon, Bajtlik (2002). This topic is generally referred to today as BAO - the use of baryonic acoustic oscillations - although in fact can be more general, i.e. make less assumptions. The best-cited example of BAO usage is AstroPh:0501171 SDSS z < 0.47 Eisenstein et al., who estimated Omega_total = 1.010\pm0.009. Updating Roukema, Mamon & Bajtlik (2002) on newer QSO redshift surveys should result in preciser, and hopefully more accurate, estimates of these metric parameters.
from within a single survey, using a standard ruler method, is AstroPh:0106135 - Roukema, Mamon, Bajtlik (2002). This topic is generally referred to today as BAO - the use of baryonic acoustic oscillations - although in fact can be more general, i.e. make less assumptions. The best-cited example of BAO usage is AstroPh:0501171 SDSS z < 0.47 Eisenstein et al., who estimated Omega_total = 1.010\pm0.009. Updating Roukema, Mamon & Bajtlik (2002) on newer QSO redshift surveys should result in preciser, and hopefully more accurate, estimates of these metric parameters. Edit | Attach | Print version | History: r2 < r1 | Backlinks | View wiki text | More topic actions
Topic revision: r2 - 06 Sep 2010, BoudRoukema
 Copyright © by the contributing authors. All material on this collaboration platform is the property of the contributing authors.
Copyright © by the contributing authors. All material on this collaboration platform is the property of the contributing authors. Ideas, requests, problems regarding Foswiki? Send feedback
