| en: |
| Exzuberant |
| In the dark |
| Trenches of discovery |
| Kipac |
| fr: |
| Café sciences |
| Luminet |
| Libération |
Fri, 22 Jan 2016
Dark energy: onus of proof reversed
 The simplest explanation for "dark energy" is that it
measures recent evolution of average negative curvature.
We think that it
mainly represents the recent formation of cosmic voids on scales of tens of
megaparsecs; these voids dominate scalar averaged quantities.
In other words,
the onus of proof has been reversed, in a
quantified way:
dark energy as something beyond classical general
relativity should be disfavoured by Occam's Razor unless a
relativistic inhomogeneous cosmological model is used.
This seems
so far to have largely gone under the radar...
The simplest explanation for "dark energy" is that it
measures recent evolution of average negative curvature.
We think that it
mainly represents the recent formation of cosmic voids on scales of tens of
megaparsecs; these voids dominate scalar averaged quantities.
In other words,
the onus of proof has been reversed, in a
quantified way:
dark energy as something beyond classical general
relativity should be disfavoured by Occam's Razor unless a
relativistic inhomogeneous cosmological model is used.
This seems
so far to have largely gone under the radar...
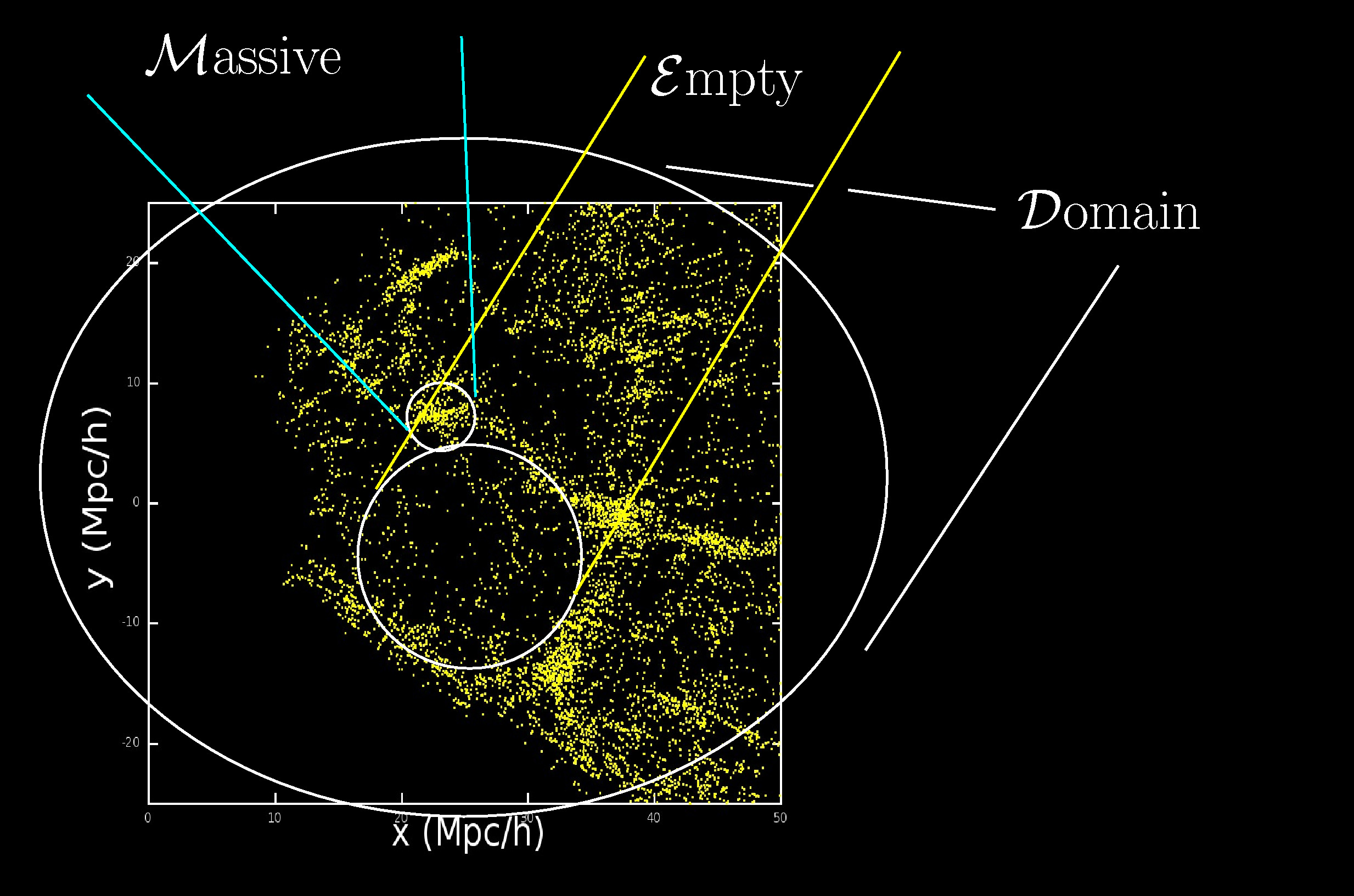
Observationally, there's no disputing the existence of dark energy in the restricted sense of providing a good observational fit to several of the main cosmological observational datasets, modulo a rather unrealistic assumption of the model used in the fitting procedure. The assumption is that the class of possible spacetimes, i.e., solutions of the Einstein equation of general relativity, is the FLRW (Friedmann-Lemaître-Robertson-Walker) family. The FLRW models require that after choosing a way to split up space and time (a foliation), the spatial slice (i.e., a 3-dimensional space) is homogeneous—the density is the same everywhere, so galaxies and voids cannot exist. In fact, cosmologists usually make a hack, modelling galaxies and voids by patching Newtonian gravity into an Einstein "background"—since using the Einstein equation is more tricky. This hack bypasses the basic problem without solving it.
Since in reality, galaxies, clusters of galaxies, the cosmic web and voids and supervoids exist beyond any reasonable doubt, the FLRW family should be expected to go wrong at recent epochs and at small (less than a few gigaparsecs) scales. And the small-scale, recent epoch is the only epoch at which a non-zero cosmological constant (or dark energy parameter ΩΛ) can (at present) be observationally distinguished from a zero cosmological constant. So it happens that just where and when we can expect things to go wrong with FLRW, ΩΛ suddenly appears, provided that we assume FLRW in our interpretation of the data despite expecting FLRW to be wrong! What is it that goes wrong? The picture above shows voids on the scales of a few tens of megaparsecs from the 2dFGRS. From a relativistic space point of view, expansion rates are different in different regions. This also happens in the hack of adding Newtonian galaxy and void formation to Einsteinian expansion, but in that case the expansion is forced to be rigid, by assumption, preventing the Einstein equation from being applied correctly. Even when we interpret the observations from a rigid comoving space point of view, the numbers show that the ratio of the "peculiar velocities" of galaxies coming out of voids to the sizes of the voids is big: several hundred km/s divided by something like 10 Mpc, giving a few times 10 km/s/Mpc. This void peculiar expansion rate is not much smaller than the Hubble constant, which is about 70 km/s/Mpc. At an order of magnitude level, the expansion rate is definitely inhomogeneous. This is why interpreting the observations in terms of homogeneous expansion gives a big error.
 In other words, unless we use a relativistic cosmological model that takes inhomogeneous
curvature and
virialisation into account,
we cannot claim that the "detected" ΩΛ
is anything other than a structure formation parameter of a fit
through cosmological data using an oversimplified fitting function.
The second picture at the right shows that going from right (early times) to
left (today), the amount of inhomogeneity (the virialisation
fraction) grows from almost nothing to a big fraction of the total mass density today.
Alternatively, if we ignore the growth in inhomogeneity, then we get
ΩΛ, interpreted from the data assuming homogeneity,
growing from almost
nothing to a big fraction (70%) of the total density today. If we ignore inhomogeneity, then
miraculously dark energy appears instead!
In other words, unless we use a relativistic cosmological model that takes inhomogeneous
curvature and
virialisation into account,
we cannot claim that the "detected" ΩΛ
is anything other than a structure formation parameter of a fit
through cosmological data using an oversimplified fitting function.
The second picture at the right shows that going from right (early times) to
left (today), the amount of inhomogeneity (the virialisation
fraction) grows from almost nothing to a big fraction of the total mass density today.
Alternatively, if we ignore the growth in inhomogeneity, then we get
ΩΛ, interpreted from the data assuming homogeneity,
growing from almost
nothing to a big fraction (70%) of the total density today. If we ignore inhomogeneity, then
miraculously dark energy appears instead!
Several relativistic structure formation cosmological models are available, though still in their infancy. However, what has been a little distracting from working on these is that some observational cosmologists thought that there existed a mathematical theorem—the Green and Wald formalism—showing that dark energy could not be a "fitting function" description of curvature and kinematical backreaction, the general-relativistic effects of treating both structure formation and expansion of the Universe together. This is why my colleagues and I had to publish a clarification showing the main flaws in this reasoning. In particular, the Green and Wald formalism is not applicable to the main relativistic structure formation cosmological models that have been proposed in the research literature over the past five years or so. Green and Wald's formalism remains an interesting contribution to the field of relativistic cosmology, but it does not "save" dark energy from being anything more exotic than spatially averaged, evolving negative curvature. After a few tweets [1] [2], a blog entry, and a reblog we can get back to work. :)
fr | permanent link | RSS | trackback: ping me (experimental)
Comments: Please publish comments on a community-based Fediverse server of your choice and ping me in the comment with @boud@framapiaf.org.
| 2020/07 |
| 2019/07 |
| 2019/04 |
| 2016/08 |
| 2016/02 |
| 2016/01 |
| home :: scalar_averaging |