Content for poster (roll-up/pull-up banner) to be printed by UMK public relations department

• keywords:
  • Kosmologia - Cosmology
  • Topologia kosmiczna - Cosmic topology
  • Kosmologia niejednorodna - Inhomogeneous cosmology
• key questions:
  • Jaki jest kształt Wszechświata? - What is the shape of the Universe?
  • Czy Wszechświat jest skończony ale nieograniczony ? - Is the Universe finite without edges?
  • Czy ciemna energia to tylko pustki kosmiczne? - Is dark energy just cosmic voids?
• Images:

• • (C) 2022 ESA/Webb CC BY 4.0
    • no text needed except for (C) 2022 ESA/Webb CC BY 4.0

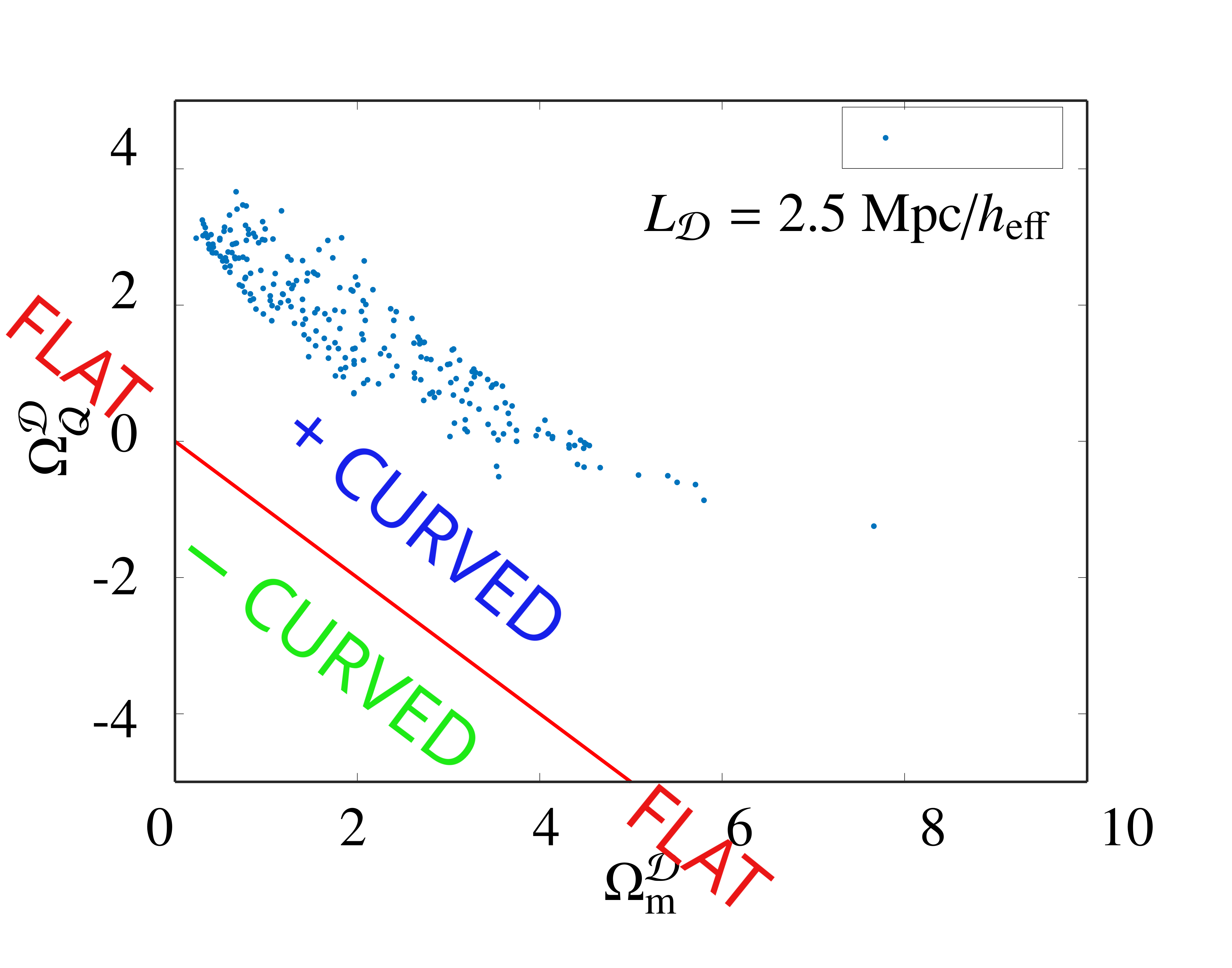• • (C) 2023 B. Roukema CC BY 4.0
    • text: Galaxies and their dark matter haloes form from small density perturbations in the expanding Universe. These overdense regions expand more slowly than the rest of the Universe and eventually "turn around" – start collapsing instead of expanding. The blue dots in this figure (for a standard ΛCDM reference model) show that at this turnaround epoch, these galaxy formation regions are positively curved. If the Universe were flat, galaxies could not be formed. Roukema & Ostrowski 2019, JCAP 12, 049 [arXiv:1902.09064], https://codeberg.org/boud/1902.09064

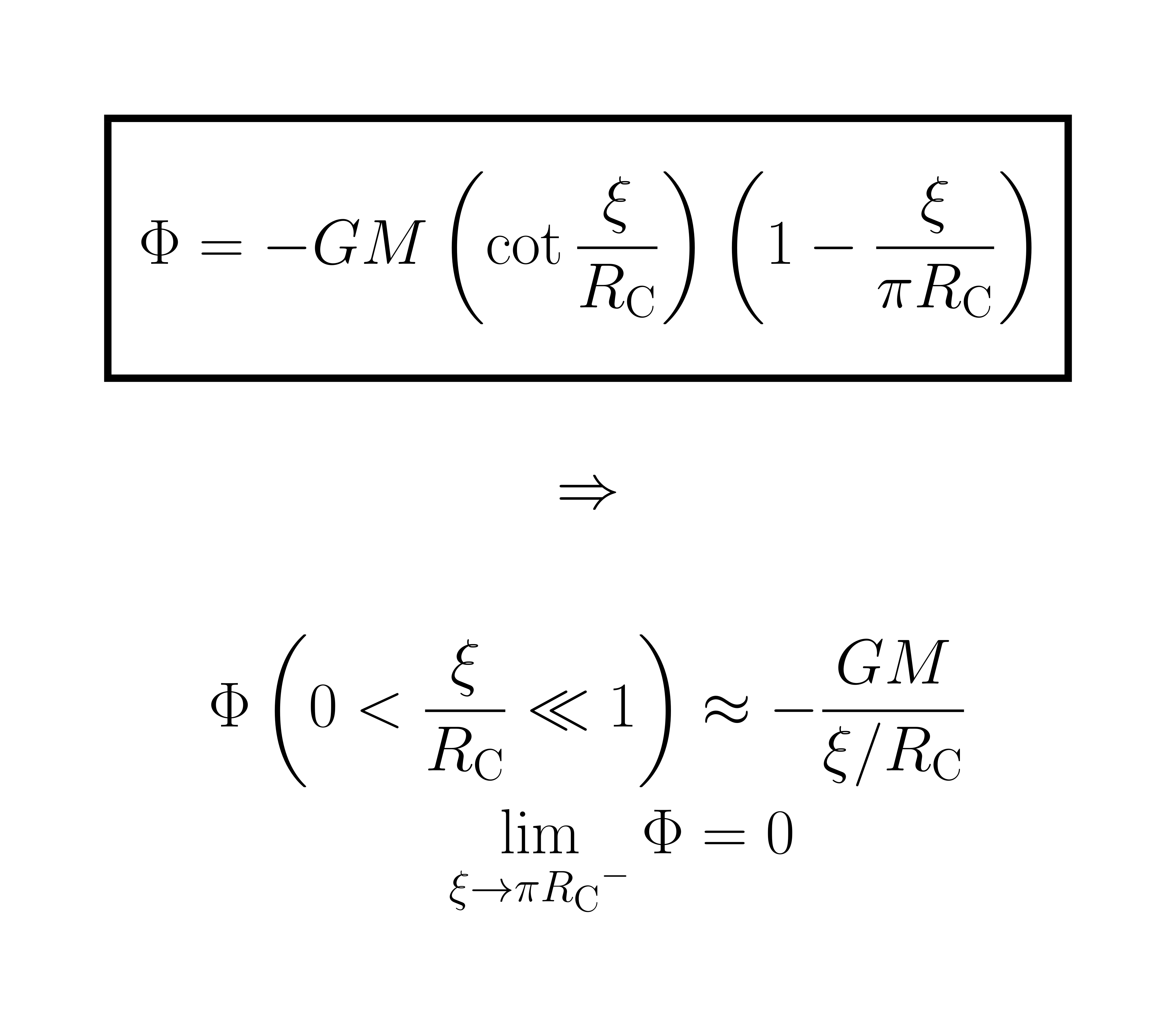
• (C) 2023 B. Roukema CC0
  • text: How can Newtonian gravitation, our non-relativistic theory of gravitation, be extended to non-Euclidean topologies? That question was answered by Vigneron (2022, CQG, 39, 155006), using a mathematical object known as Galilean structure. This "non-Euclidean Newtonian theory of gravitation" predicts, in particular, how the topology of the Universe influences the gravitational potential created by a massive object. If the space of our Universe has hyperspherical curvature, then Newton's law written as a potential, i.e. −GM/r, is not valid and must be replaced by the formula above at a distance ξ, where R_C is the hyperspherical radius (and a closed straight circle has length 2πR_C). While the observational effect of the difference with Newton's law is likely to be tiny, this formula shows that the topology of the Universe, can, in principle, be measured, no matter how big the Universe is. Vigneron & Roukema 2022, PRD 107, 063545 [arXiv:2201.09102], https://codeberg.org/boud/topoaccel

What is a "roll-up banner"?

• Searx q=marketing+roll+up+screen

LaTeX source for an example pull-up banner

\documentclass[portrait]{sciposter}

\renewcommand{\papertype}{custom}
\renewcommand{\fontpointsize}{25pt}
\renewcommand{\paperwidth}{800mm}
\renewcommand{\paperheight}{2000mm}
\renewcommand{\setpspagesize}{
  \ifthenelse{\equal{\orientation}{portrait}}
    \special{papersize=800mm,2000mm}
    }{\special{papersize=2000mm,800mm}
}

%hacks
\setlength{\textheight}{1990mm}
\setlength{\textwidth}{770mm}
\setlength{\oddsidemargin}{-35mm}

%\usepackage{fontspec} % xelatex|lualatex
\usepackage{fix-cm}
\usepackage{multicol}
\usepackage{graphicx}
\usepackage{hyperref}
\usepackage{suffix}
\usepackage{setspace}
\usepackage{textpos}
\usepackage[polish]{babel}
\usepackage[LGR,T1]{fontenc}
%\usepackage[T2A]{fontenc}
\usepackage[utf8]{inputenc}
\usepackage{polski}
%\usepackage{url}

\usepackage{lmodern}
%\newfontfamily\mydejavu{DejaVu Sans}

\newcommand\mytitlesize{\fontsize{70mm}{6mm}\selectfont}

\newcommand\keyquestionsone{\fontsize{35mm}{3mm}\selectfont}
\newcommand\keyquestionstwo{\fontsize{25mm}{3mm}\selectfont}

\newcommand\legendone{\fontsize{20mm}{30mm}\selectfont}
\newcommand\legendoneref{\fontsize{15mm}{2mm}\selectfont \it}
\newcommand\legendtwo{\fontsize{20mm}{3mm}\selectfont}
\newcommand\legendtworef{\fontsize{15mm}{2mm}\selectfont \it}

\newcommand\myvspace{\rule{0ex}{2ex}}

\begin{document}

{\centering
  \mytitlesize Kosmologia

  \myvspace

}

%\maketitle


\begin{figure}
  \centering
  \includegraphics[width=\textwidth]{Webb}

  {\normalsize (C) 2022 ESA/Webb CC BY 4.0}

\end{figure}

\myvspace

{\centering

  \keyquestionsone
  Jaki jest kształt Wszechświata?

  {\it What is the shape of the Universe?}

  \myvspace

  Czy Wszechświat jest skończony ale nieograniczony ?

  {\it Is the Universe finite without edges?}

  \myvspace

  Czy ciemna energia to tylko pustki kosmiczne?

  {\it Is dark energy just cosmic voids?}

  \myvspace

}


\begin{multicols}{2}

  \begin{figure}

    {\centering

      {\keyquestionstwo
        Kosmologia niejednorodna}

      \includegraphics[width=0.88\textwidth]{RO19_rerun_Fig6a}

      {\keyquestionstwo \it Inhomogeneous cosmology}

      \myvspace

      \myvspace

    }


    {\legendone
    Galaxies and their dark matter haloes form from small density perturbations in the expanding Universe. These overdense regions expand more slowly than the rest of the Universe and eventually ``turn around'' -- start collapsing instead of expanding. The blue dots in this figure (for a standard $\Lambda$CDM reference model) show that at this turnaround epoch, these galaxy formation regions are positively curved. If the Universe were flat, galaxies could not be formed.}
    {\legendoneref
    Roukema \& Ostrowski 2019, JCAP 12, 049 [arXiv:1902.09064], https://codeberg.org/boud/1902.09064}
  \end{figure}

  \begin{figure}

    {\centering

      {\keyquestionstwo
        Topologia kosmiczna}

      \includegraphics[width=0.88\textwidth]{NEN}

      {\keyquestionstwo
        \it Cosmic topology}

      \myvspace

      \myvspace

    }

    {\legendtwo
    How can Newtonian gravitation, our non-relativistic theory of gravitation, be extended to non-Euclidean topologies? That question was answered by Vigneron (2022, CQG, 39, 155006), using a mathematical object known as Galilean structure. This ``non-Euclidean Newtonian theory of gravitation'' predicts, in particular, how the topology of the Universe influences the gravitational potential created by a massive object. If the space of our Universe has hyperspherical curvature, then Newton's law written as a potential, $-GM/r$, is not valid and must be replaced by the formula above at a distance $\xi$, where $R_\mathrm{C}$ is the hyperspherical radius (and a closed straight circle has length 2$\mathrm{\pi}R_{\mathrm{C}}$). While the observational effect of the difference with Newton's law is likely to be tiny, this formula shows that the topology of the Universe, can, in principle, be measured, no matter how big the Universe is.}
    {\legendtworef
    Vigneron \& Roukema 2022, PRD 107, 063545 [arXiv:2201.09102], https://codeberg.org/boud/topoaccel}
  \end{figure}
\end{multicols}

{\centering

  \myvspace

  \myvspace

  \mytitlesize Cosmology

  \keyquestionsone [$+$ logo UMK, ,,Instytut Astronomii'', \ldots]

}




\end{document}