Wed 16 Sep 2009 - Lotte + Heller

Renate LOTTE - CDT (Causal Dynamical Triangulation) QG

• • "euclidean" path integrals give different (wrong) results compared to lorentzian path integrals - causality is necessary for doing this properly
    • Wick rotation
  • trying to build up a 4D model
    • euclideanised: get phases with Hausdorff dimension infinity or 2
    • lorentzian: 3 phases - "A, B, C" - phase C is the cosmologically interesting phase
    • figure "dynamically generated 4-d quantum universe, obtained from a causal path integral"
  • results:
    • casuality is not emergent, must be assumed as microcausality on each spacetime history
    • time is not emergent, must be assumed
  • "CDT is the only theory of QG where a classical extended geometry is generated from Planck-scale ecitations"
    • e.g. hep-th/0505113 with Jurkiewicz, ...
    • topology and dimensionality become dynamical in QT; can happen because
      • short-scale fluctuations are large
      • we are taking a nontrivial continuum limit
    • "contribution from 'microstates' is crucial for obtaining de Sitter space"
  • thesis: "there is a unique interacting quantum (field) theory of spacetime geometry in 4D, which has GR as its classical limit"
    • if thesis true, then CDT approach has a good chance of finding this
  • Review papers on this: ArXiv:0711.0273, HepTh:0604212, HepTh:0509010 (hep-th/0604212, hep-th/0509010)
  • http://www.phys.uu.nl/~loll

Michal HELLER - noncommutative Friedman cosmology model

• • generation of matter; singularities
  • transformation groupoid:
    • \Gamma = E \times G (G = Lorentz group); \gamma \in \Gamma are pairs (p,g)
    • -> E = frame bundle
    • -> M = space-time
    • but considers Lorentz transformations as more fundamental than space-time
  • \Gamma_1 = E \times E, \gamma = (p_1, p_2) = pair groupoid
    • \Gamma_1 and \Gamma are isomorphic
  • algebra
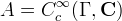
    • compact support, convolution is multiplication
    • 
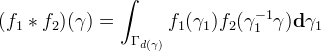
    • Z(A) = 0 - the center of the group is zero
    • "outer centre" defined
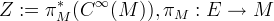
    • \alpha: Z \times A \rightarrow A
    • 
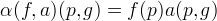
  • info on GR + QG contained in differential algebra (A, DerA)
    • 
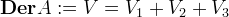
      • V_1 "horizontal" - lifted from M with the help of the connection
      • V_2 "vertical" - projecting to zero on M
      • V_3 "InnA" = {ad a: a \in A}
      • V_1 circplus V_2 - gravitational sector
      • V_3 - quantum sector
  • gravitational sector
  • 3. universe
    • M = (0,T) \times S^3
    • E = M \times R
    • G = ...
    • \Gamma = ...
    • A = ...
    • Einstein equation now becomes eigenvalue type problem
      • 
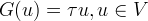
      • eigenvalues \tau_B and \tau_h give standard stress-energy tensor
      • \tau_Q = 1/2 \tau_B + 3/2 \tau_h
        • \tau_Q = 4\pi G\rho - dust
        • \tau_Q = 0 - radiation